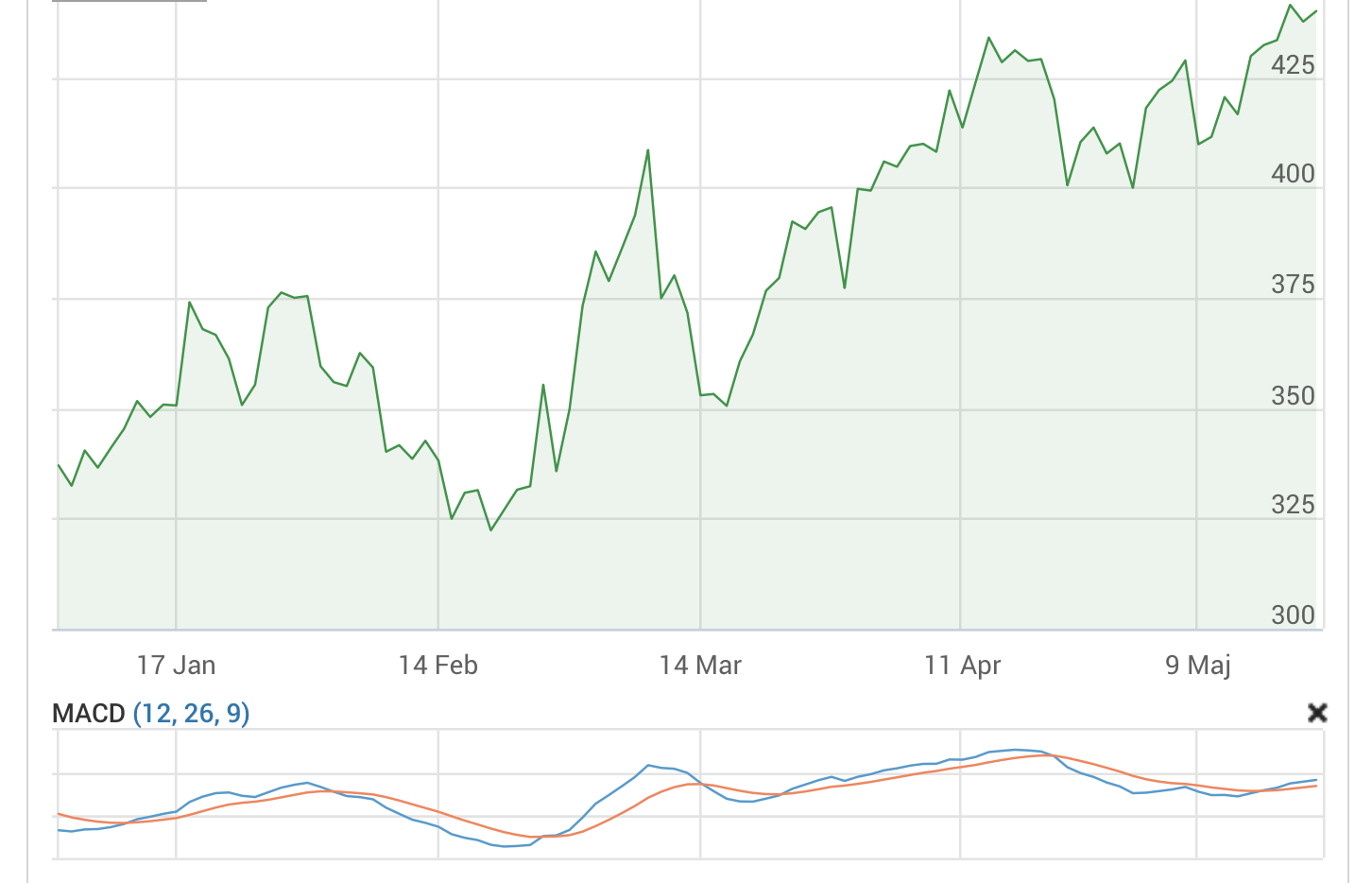
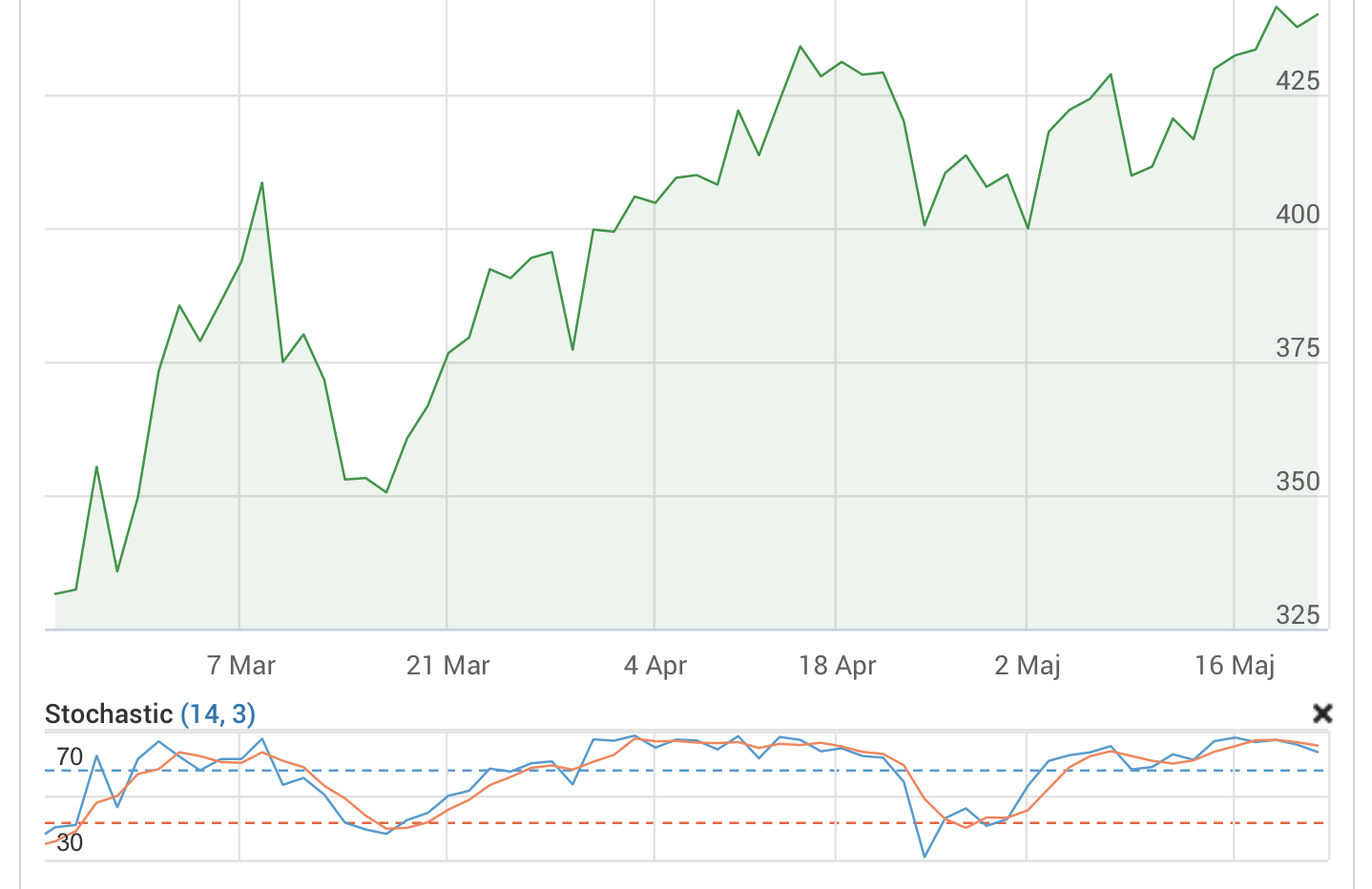
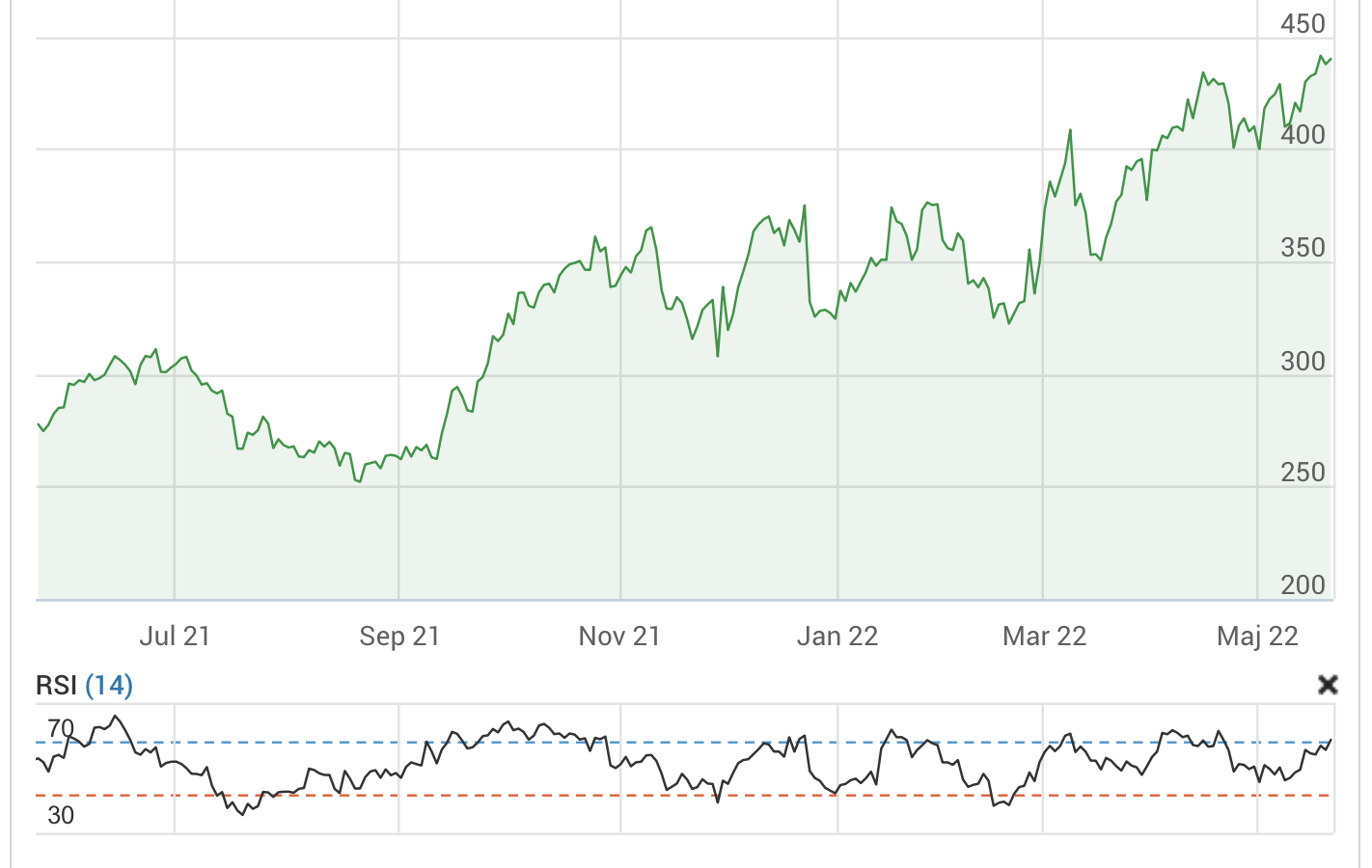
Analys Bilia
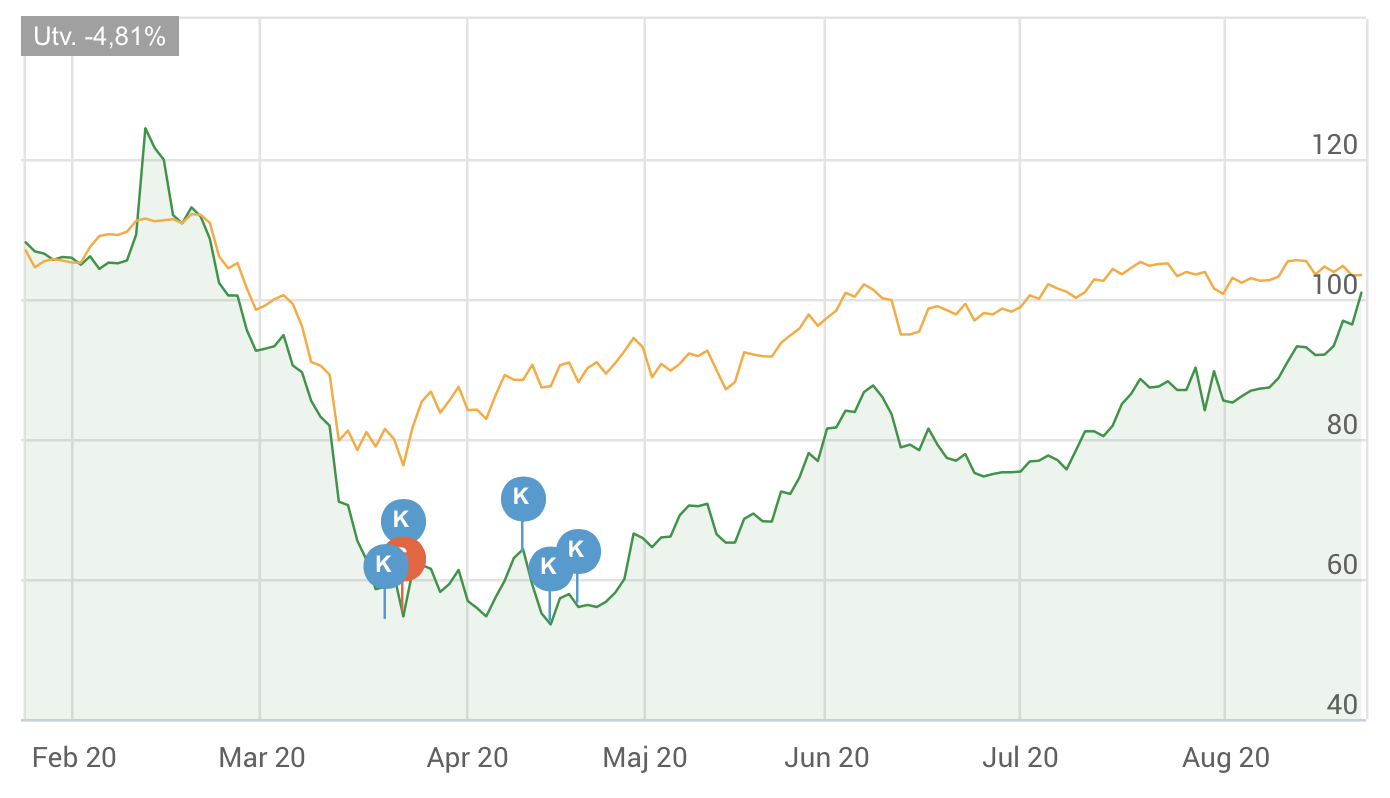
Bilia var ett av de bolag jag plockade upp i våras. De drogs med i corona-raset och föll som mest med nästan 60 procent. Det var överdrivet i mina ögon, så jag ackumulerade en bra size under slutet av mars och april. Jag har haft dem på radarn länge, men det har aldrig blivit av. Stora insiderköp blev utlösande faktorn denna gången att köpa. Som de flesta andra bolag följde Bilia med upp när börsen återhämtade sig. Bilia är en av Europas största bilåterförsäljare med en ledande position inom både service och försäljning av nya och begagnade person- och transportbilar samt tilläggstjänster som finansiering och försäkring. Bolaget har 136 anläggningar med cirka 5 000 medarbetare i Sverige, Norge, Tyskland, Luxemburg och Belgien samt två internetbaserade auktionssajter. 2019 omsatte koncernen 29.5 miljarder kronor, varav 40 procent utanför Sverige. Bilia påverkades framför allt negativt av ras i nybilsförsäljningen, medan serviceaffären är ganska intakt. Förra året (2019) stod serviceaffären för 70 … Läs mer