Halvårsavstämning 2025
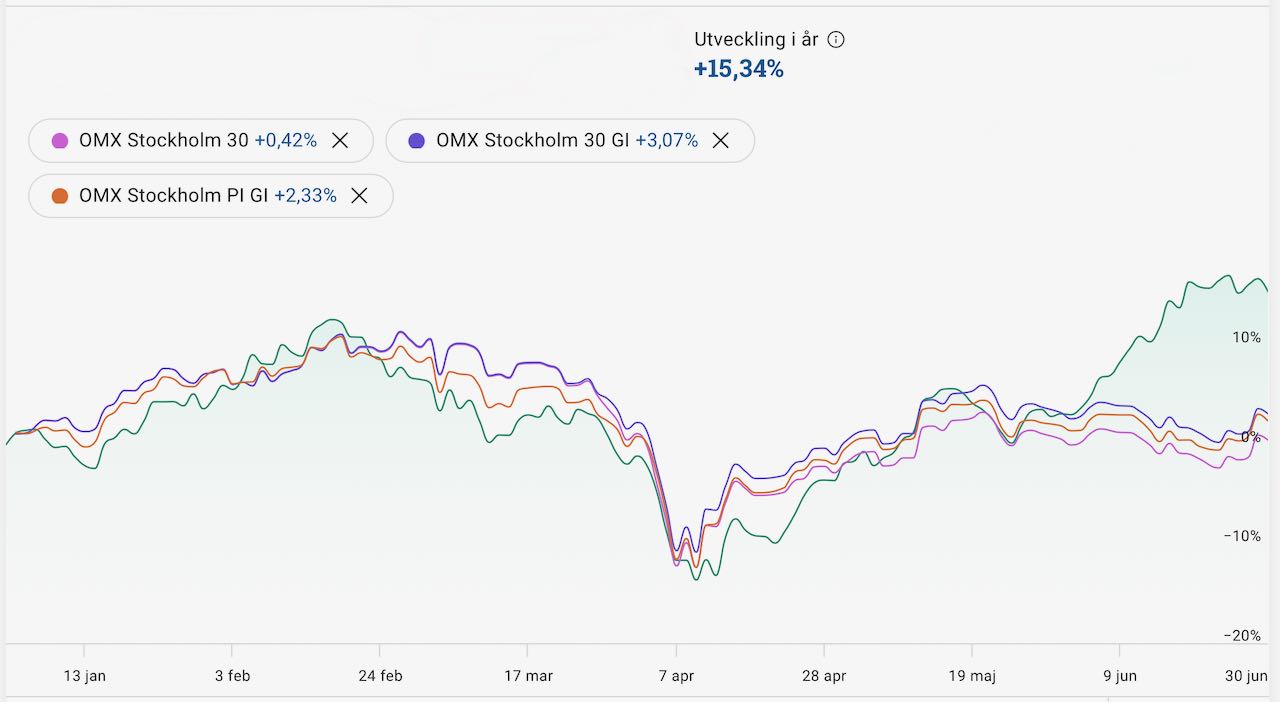
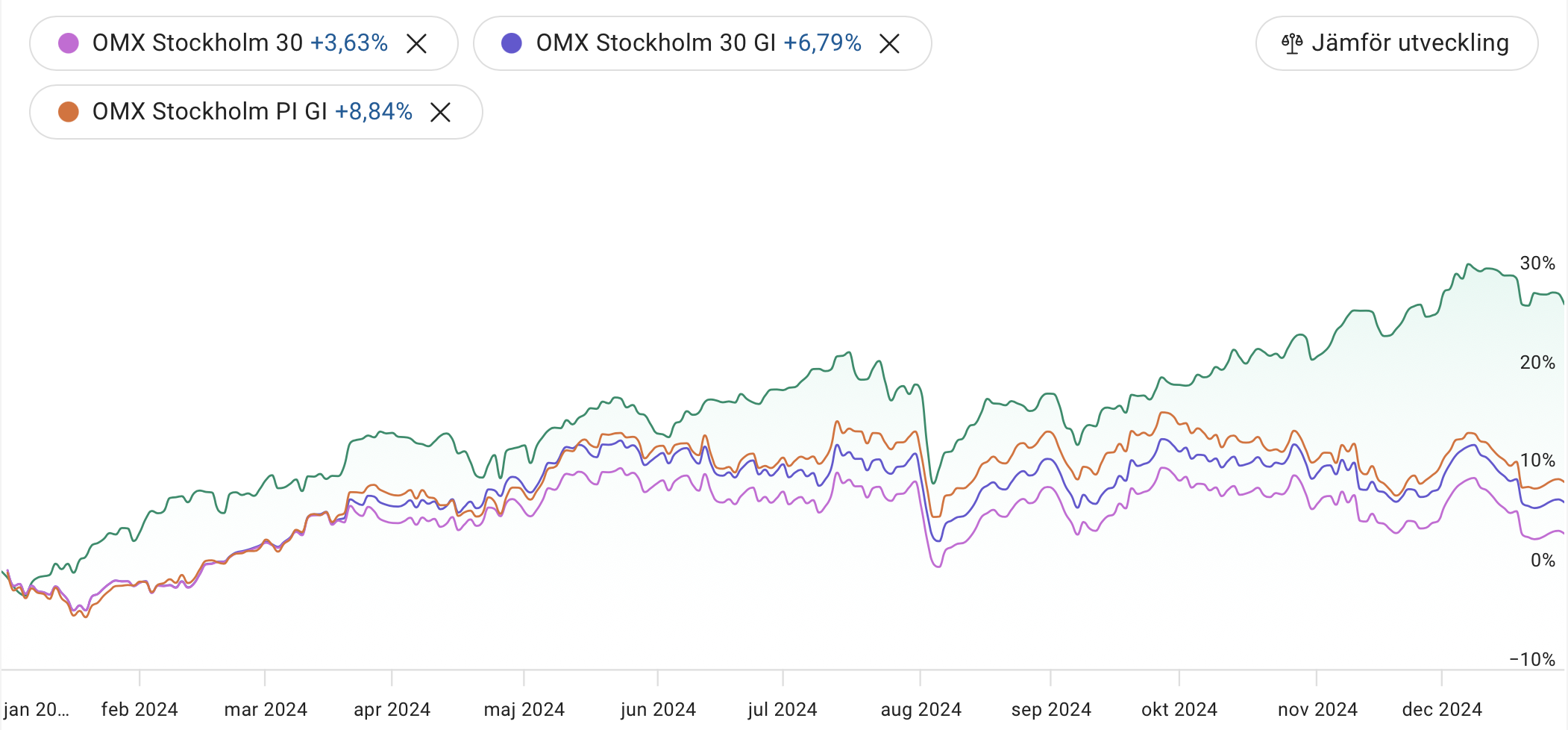
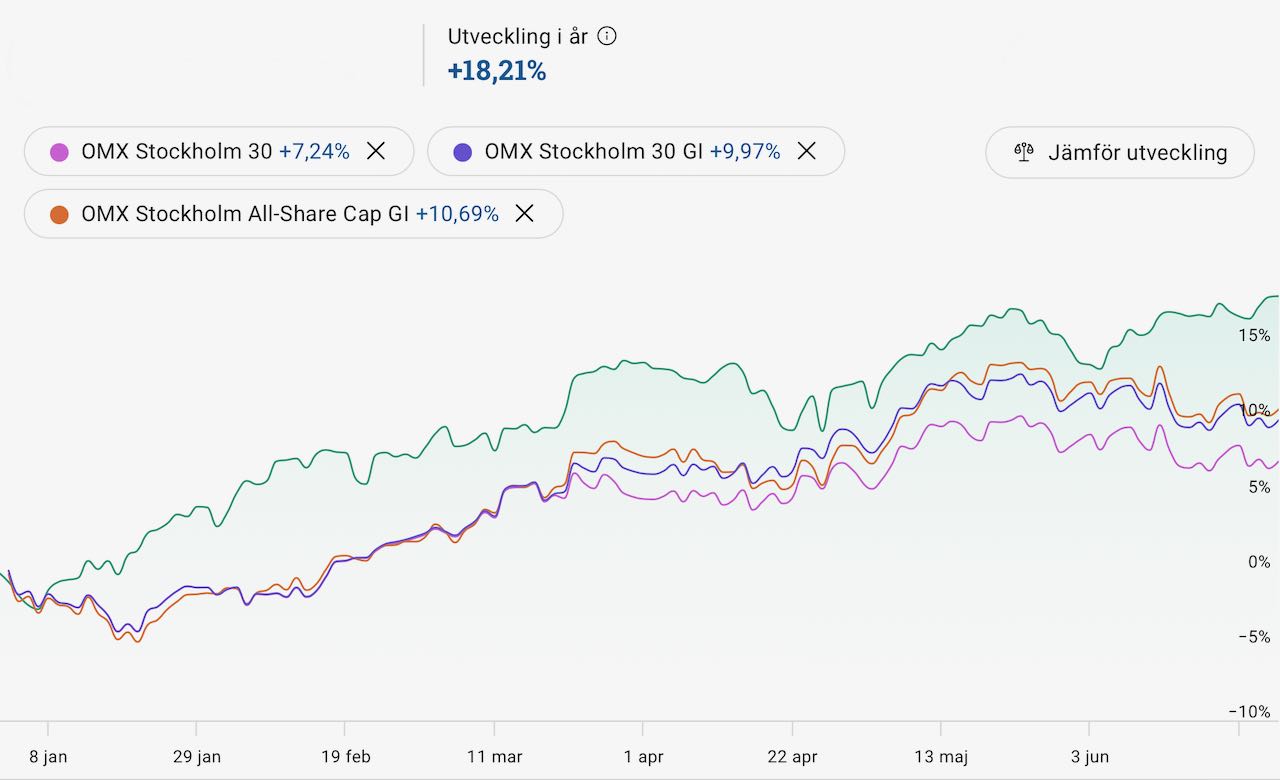
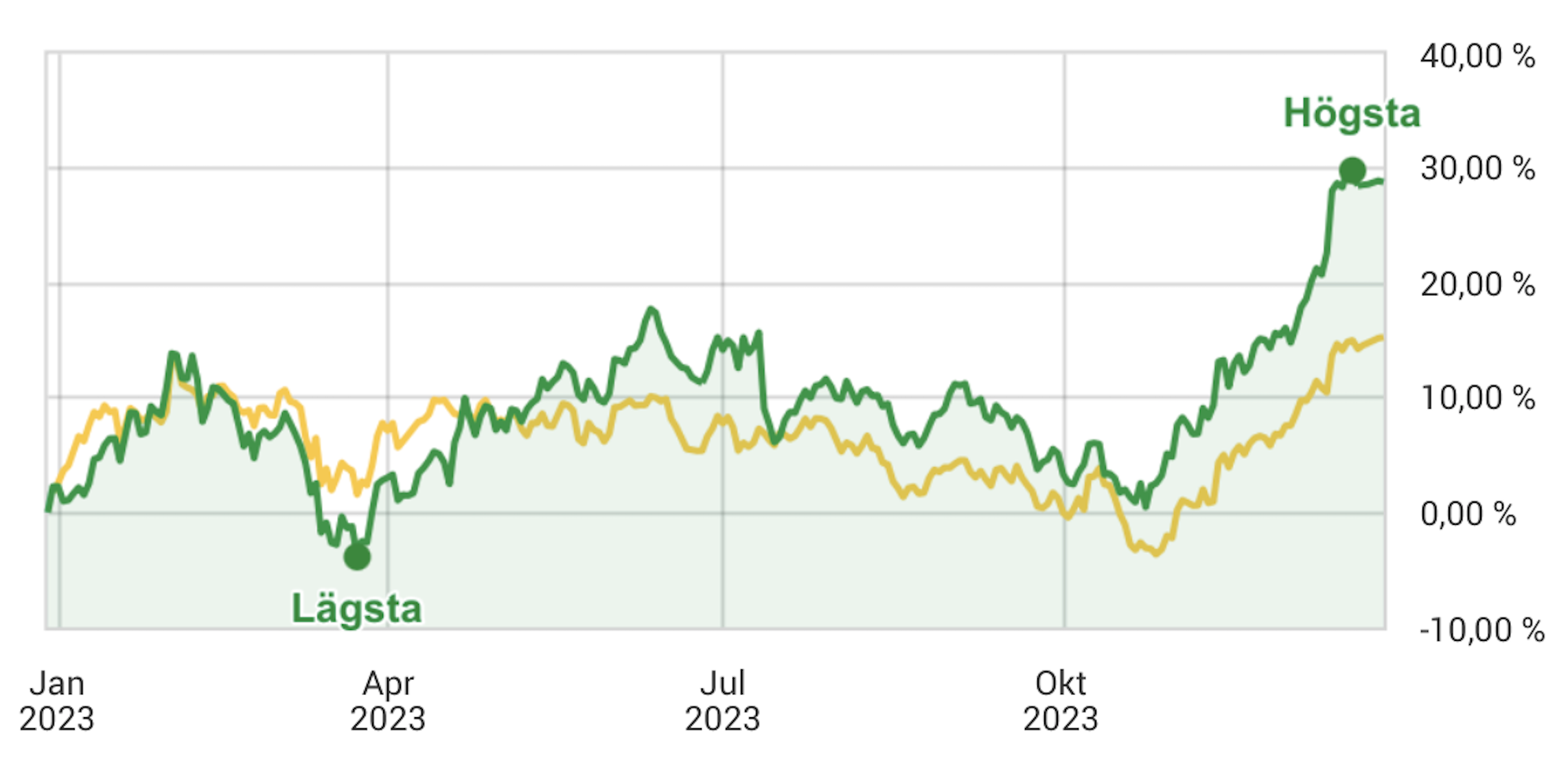
Sommaren är här, dags för halvårsavstämning 2025. Huvudportföljen The Mother Ship är upp +15 procent YTD (+24 procent YoY). De breda indexen ligger runt 0 till +3 procent YTD. Lite alfa-avkastning på slutet där alltså. De största bidragen kommer från Aker BP (+21 procent med utdelning) och Netflix (+50 procent) samt uppstickaren och riskinnehavet AST Space Mobile som rusat hela 121 procent i år och 302 procent på 12 månader. Aker BP är ett norskt energibolag inom olja och gas. De förvärvade Lundin Energy 2021. Om efterfrågan på olja inte är noll om 15–20 år är Aker BP billigt. Under tiden får man en direktavkastning på nästan 10 procent. Vi får se. AST bygger rymdbaserat mobilnätverk för vanliga mobiltelefoner. Bolaget är pre-revenue och hög risk. Allas favoritfilmkanal Netflix är nu upp 500 procent sedan jag fiskade upp dem när Bill Ackman sålde. Kul när bottenfiske klaffar, men annars är det inget jag rekommenderar att försöka … Läs mer